مجله ریاضی
گشتی در دنیای زیبای ریاضیات
مجله ریاضی
گشتی در دنیای زیبای ریاضیاتدرباره من
وبلاگ رسمی اصغر ناصری
این وبلاگ با هدف ارائه مطالب آموزشی تهیه می شود و قصد دارد به دانشنامه کوچکی از علوم و فنون تبدیل گردد.
ادامه...
مسایل و معادلات جالب ریاضی (1)
همه معادلات ریاضی دارای راه حل کلاسیک و سرراست نیستند. برخی از آنها نیاز به راه حل های ابتکاری دارند که در پایان به برابری‌های ساده ای می انجامد.
با استفاده از ماشین حساب این مساله به راحتی قابل حل است اما می‌خواهیم راه حلی جبری برای آن پیدا کنیم. ابتدا به معادله ساده زیر و جواب آن توجه می‌کنیم.
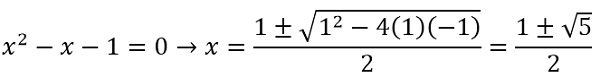
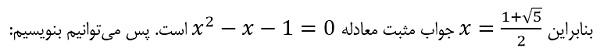
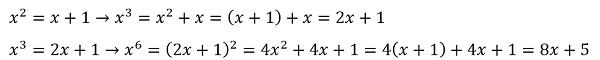
توجه کنید که همه جا به جای عبارت توان دو از معادل آن استفاده کرده ایم.
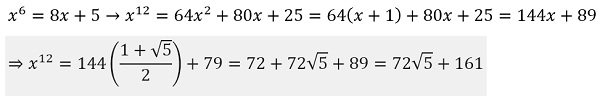
آیا راه حل ساده تری برای این مساله در دست دارید؟ برای ما ارسال کنید.
معادلات تابعی
یکی از مسایل جالب آنالیز ریاضی، معادلات تابعی هستند. منظور از یک معادله تابعی، یک تساوی بین مقادیر مختلف یک تابع در آرگومانهای مختلف است. در این نوشتار برای ورود به این مبحث جالب، یک معادله تابعی نمونه را طرح و حل می کنیم.
- تابع f(x) را به گونه ای تعیین کنید که f(x+f(y))=x+y+1
حل: با قراردادن y=0 خواهیم داشت:
f(x+f(0))=x+1
اگر f(0)=c فرض کنیم داریم f(x+c)=x+1 بنابراین f(x)=x-c+1
از آخرین تساوی خواهیم داشت f(0)=-c+1 بنابراین:
f(0)=c , f(0)=-c+1 -> c=-c+1 -> 2c=1 -> c=1/2
بنابراین
f(x)=x-1/2+1 -> f(x)=x+1/2
معادلات تابعی مسایل خوبی برای نوآوری و ابتکار هستند. این گونه مسایل راه حل کلاسیک ندارند و هرکدام نیاز به راه حل خلاقانه جداگانه‌ای دارند.
طرح و بحث: اصغر ناصری، مدرس خصوصی ریاضیات دبیرستان و دانشگاه - 09360771981