مجله ریاضی
گشتی در دنیای زیبای ریاضیات
مجله ریاضی
گشتی در دنیای زیبای ریاضیاتاتحادهای مثلثاتی
نمونه مسایل اتحادها و روابط مثلثاتی، قابل استفاده برا ی دانش آموزان دبیرستان
سری های مثلثاتی و نحوه محاسبه آنها
سری های مثلثاتی مبحث بسیار جالبی در مثلثات پایه است که با وجود اهمیت و کاربرد انها در مباحث فیزیک دانشگاه، از کتابهای نظام جدید آموزش نظام جدید متوسطه حذف شده است. این نوشتار به معرفی چند سری مثلثاتی و شیوه محاسبه مجموع آنها برای دانش |آموزان علاقمند به ریاضی می پردازد.
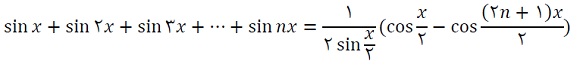
مسایل حل نشده در دنیای ریاضیات - فرضیه ریمان
امروزه بیشتر ریاضیدانان بر این باورند که فرضیه ریمان یکی از مهمترین مسایل در تمامی ریاضیات بشمار می رود. یکی از هفت مساله هزاره که برای حل آن یک میلیون دلار جایزه تعیین شده است. این مساله کاربرد زیالدی در شاخه های مختلف ریاضیات دارد، با این وجود بر مبنای ساده ای بنا شده است.
تابعی به نام تابع زتای ریمان وجود دارد که تصویر آن را در زیر می بینید:
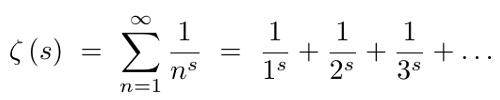
برای s = 2 به مجموع نامتناهی زیر می رسیم که با عملیات ریاضی نه چندان دشواری به پاسخ مشهوری می رسد:
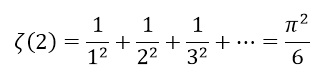
اما اگر s عددی مختلط مانند a+ib باشد، محاسبه این سری عملی بی نهایت دشوار می شود که تاکنون راهی برای آن پیدا نشده است. بویژه یافتن ریشه های تابع زتا مساله بسیار غامضی است. صورت رسمی فرضیه ریمان چنین است: "هر ریشه تابع زتا دارای بخش حقیقی 1/2 است". اگر برای فرضیه ریمان پاسخی پیدا شود، یکی از موانع مهم بر سر راه پیشبرد نظریه اعداد برداشته خواهد شد.
مسایل حل نشده در دنیای ریاضیات - حدس کولاتز
ریاضیدانان از باهوش ترین انسانهای روی کره زمین هستند. لیکن هنوز مسایل بسیاری در ریاضیات وجود دارد که با وجود ظاهر ساده شان غیرقابل حل باقی مانده اند. یکی از آنها حدس کولاتز یا Collatz Conjecture است.
تابع زیر را در نظر بگیرید:
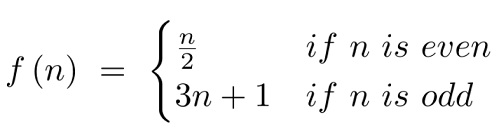
این تابع هر عدد زوج را نصف کرده و عدد فرد را سه برابر ساخته و عدد یک را به آن می افزاید. اگر این تابع را بطور متوالی بر هر عدد زوج اعمال کنید در نهایت به عدد یک می رسید. برای مثال:
f(5)=3(5)+1=16 , f(f(5))=f(16)=8 , f(f(f(5)))=f(8)=4 , f(f(f(f(5))))=f(4)=2 , f(f(f(f(f(5)))))=f(2)=1
آیا این موضوع برای تمامی اعداد طبیعی صادق است؟ هنوز نمی دانیم. 82 سال است که دانشمندان هنوز راه حل این مساله را نیافته اند!
منبع: Popular Mechanics
مسایل و معادلات جالب ریاضی (1)
همه معادلات ریاضی دارای راه حل کلاسیک و سرراست نیستند. برخی از آنها نیاز به راه حل های ابتکاری دارند که در پایان به برابریهای ساده ای می انجامد.

با استفاده از ماشین حساب این مساله به راحتی قابل حل است اما میخواهیم راه حلی جبری برای آن پیدا کنیم. ابتدا به معادله ساده زیر و جواب آن توجه میکنیم.
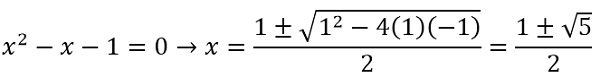
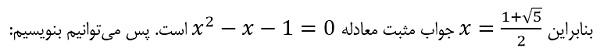
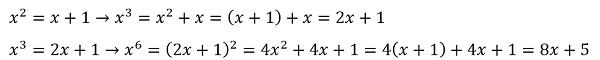
توجه کنید که همه جا به جای عبارت توان دو از معادل آن استفاده کرده ایم.
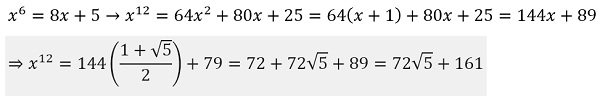
آیا راه حل ساده تری برای این مساله در دست دارید؟ برای ما ارسال کنید.